2D Physics Simulation

The goal of this project was to create a simulation of a 6 DoF system modeled using Lagrangian dynamics. The system consists of a large “box” body with a small “jack” body inside of it where each body is free to translate in two directions and rotate about one axis.

Demo

Setup

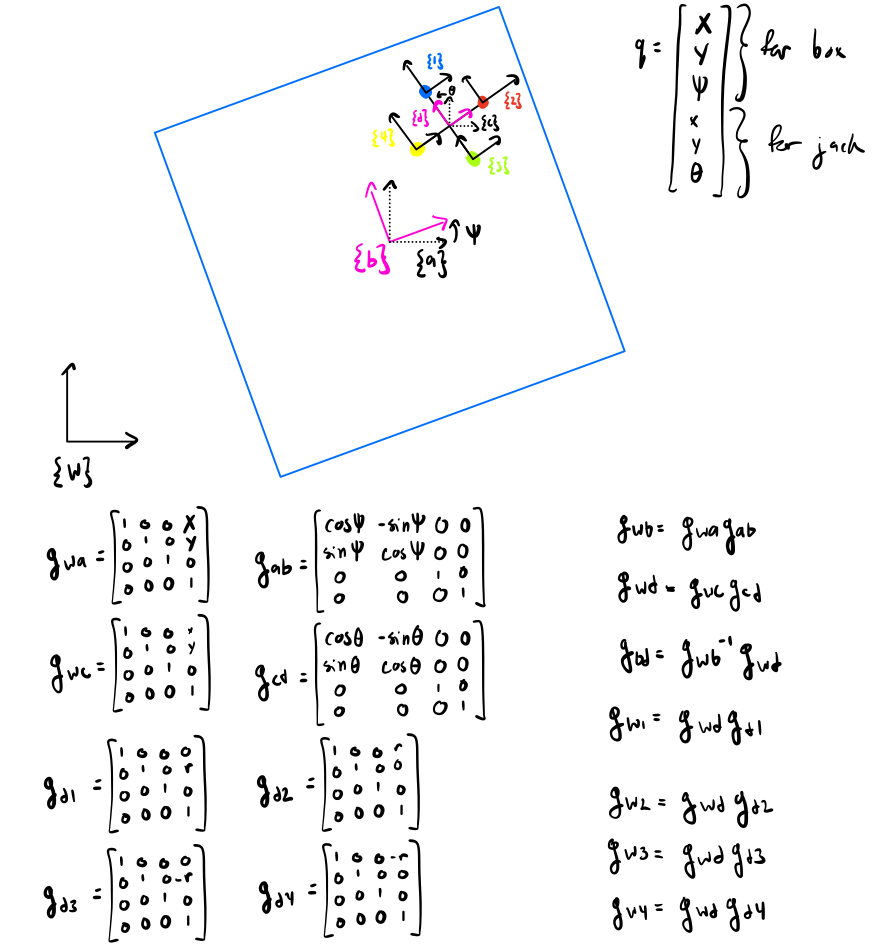
The first steps taken in this project consisted of setting up transformation matrices between the world, jack, and box frames. These matrices are used to make the necessary calculations of easier. A diagram of the system with the transformation matrices can be seen below.

Lagrangian Dynamics

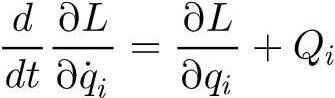
The forced Euler-Lagrange equations (shown above) were used to calculate the instaneous accelerations of the bodies that are essential for simulating the system. The Lagrangian (L) can be calculated by finding the body velocities of the box and the jack, defining the inertial matrices, and calculating the kinetic energy and potential energy. In this simulation, external forces (Qi in the equations above) are applied to Y-coordinate and psi-coordinate of the box to keep it around the same height throughout the simulation. Using the Lagrangian and external forces, the equation shown above can be calculated for each component of the configuration q. From these equations, the accelerations of the configuration are found, and the system is simulated using 4th-order Runge-Kutta integration over a 0.01 second timestep.

Impacts

In order to include elastic impacts in the simulation of this system, the locations of each of the 4 masses on the jack were checked to see if they had come in contact with the box walls at each timestep. If the jack had come in contact with the box, then the velocities of the bodies were updated appropriately using impact update equations involving the Hamiltonian and momentum.